En estadística, grados de libertad
es un estimador del número de categorías independientes en una prueba
particular o experimento estadístico. Se encuentran mediante la fórmula  , donde
, donde 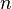 =número de sujetos en la muestra (también pueden ser representados por
=número de sujetos en la muestra (también pueden ser representados por  , donde
, donde  =número de grupos, cuando se realizan operaciones con grupos y no con sujetos individuales) y
=número de grupos, cuando se realizan operaciones con grupos y no con sujetos individuales) y  es el número de sujetos o grupos estadísticamente dependientes.
es el número de sujetos o grupos estadísticamente dependientes.
 , donde
, donde 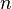 =número de sujetos en la muestra (también pueden ser representados por
=número de sujetos en la muestra (también pueden ser representados por  , donde
, donde  =número de grupos, cuando se realizan operaciones con grupos y no con sujetos individuales) y
=número de grupos, cuando se realizan operaciones con grupos y no con sujetos individuales) y  es el número de sujetos o grupos estadísticamente dependientes.
es el número de sujetos o grupos estadísticamente dependientes.
Cuando se trata de ajustar modelos estadísticos a un conjunto de
datos, los residuos -expresados en forma de vector- se encuentran
habitualmente en un espacio de menor dimensión que aquél en el que se
encontraban los datos originales. Los grados de libertad del error los
determina, precisamente, el valor de esta menor dimensión.
Un ejemplo aclara el concepto. Supongamos que
 son variables aleatorias, cada una de ellas con media
son variables aleatorias, cada una de ellas con media  , y que
, y que
es la "media muestral". Entonces las cantidades

son los residuos, que pueden ser considerados estimaciones de los errores  . La suma de los residuos (a diferencia de la suma de los errores, que no es conocida) es necesariamente 0,
. La suma de los residuos (a diferencia de la suma de los errores, que no es conocida) es necesariamente 0,
 . La suma de los residuos (a diferencia de la suma de los errores, que no es conocida) es necesariamente 0,
. La suma de los residuos (a diferencia de la suma de los errores, que no es conocida) es necesariamente 0,
ya que existen variables con valores superiores e inferiores a la
media muestral. Esto también significa que los residuos están
restringidos a encontrarse en un espacio de dimensión  (en este ejemplo, en el caso general a
(en este ejemplo, en el caso general a  ) ya que, si se conoce el valor de
) ya que, si se conoce el valor de  de estos residuos, la determinación del valor del residuo restante es inmediata. Así, se dice que "el error tiene
de estos residuos, la determinación del valor del residuo restante es inmediata. Así, se dice que "el error tiene  grados de libertad" (el error tiene
grados de libertad" (el error tiene  grados de libertal para el caso general)..
grados de libertal para el caso general)..
 (en este ejemplo, en el caso general a
(en este ejemplo, en el caso general a  ) ya que, si se conoce el valor de
) ya que, si se conoce el valor de  de estos residuos, la determinación del valor del residuo restante es inmediata. Así, se dice que "el error tiene
de estos residuos, la determinación del valor del residuo restante es inmediata. Así, se dice que "el error tiene  grados de libertad" (el error tiene
grados de libertad" (el error tiene  grados de libertal para el caso general)..
grados de libertal para el caso general)..
No hay comentarios:
Publicar un comentario