En un estudio de investigación, el error de tipo I también denominado error de tipo alfa (α) o falso positivo, es el error que se comete cuando el investigador no acepta la hipótesis nula ( ) siendo ésta verdadera en la población.
Es equivalente a encontrar un resultado falso positivo, porque el
investigador llega a la conclusión de que existe una diferencia entre
las hipótesis cuando en realidad no existe. Se relaciona con el nivel de
significancia estadística.
) siendo ésta verdadera en la población.
Es equivalente a encontrar un resultado falso positivo, porque el
investigador llega a la conclusión de que existe una diferencia entre
las hipótesis cuando en realidad no existe. Se relaciona con el nivel de
significancia estadística.
 ) siendo ésta verdadera en la población.
Es equivalente a encontrar un resultado falso positivo, porque el
investigador llega a la conclusión de que existe una diferencia entre
las hipótesis cuando en realidad no existe. Se relaciona con el nivel de
significancia estadística.
) siendo ésta verdadera en la población.
Es equivalente a encontrar un resultado falso positivo, porque el
investigador llega a la conclusión de que existe una diferencia entre
las hipótesis cuando en realidad no existe. Se relaciona con el nivel de
significancia estadística.
La hipótesis de la que se parte  aquí es el supuesto de que la situación experimental presentaría un
«estado normal». Si no se advierte este «estado normal», aunque en
realidad existe, se trata de un error estadístico tipo I. Algunos
ejemplos para el error tipo I serían:
aquí es el supuesto de que la situación experimental presentaría un
«estado normal». Si no se advierte este «estado normal», aunque en
realidad existe, se trata de un error estadístico tipo I. Algunos
ejemplos para el error tipo I serían:
 aquí es el supuesto de que la situación experimental presentaría un
«estado normal». Si no se advierte este «estado normal», aunque en
realidad existe, se trata de un error estadístico tipo I. Algunos
ejemplos para el error tipo I serían:
aquí es el supuesto de que la situación experimental presentaría un
«estado normal». Si no se advierte este «estado normal», aunque en
realidad existe, se trata de un error estadístico tipo I. Algunos
ejemplos para el error tipo I serían:- Se considera que el paciente está enfermo, a pesar de que en realidad está sano; hipótesis nula: El paciente está sano.
- Se declara culpable al acusado, a pesar de que en realidad es inocente; hipótesis nula: El acusado es inocente.
- No se permite el ingreso de una persona, a pesar de que tiene derecho a ingresar; hipótesis nula: La persona tiene derecho a ingresar.
Errores en el contraste
Una vez realizado el contraste de hipótesis, se habrá optado por una de las dos hipótesis, la hipótesis nula o base  o la hipótesis alternativa
o la hipótesis alternativa  ,
y la decisión escogida coincidirá o no con la que en realidad es
cierta. Se pueden dar los cuatro casos que se exponen en el siguiente
cuadro:
,
y la decisión escogida coincidirá o no con la que en realidad es
cierta. Se pueden dar los cuatro casos que se exponen en el siguiente
cuadro:
 o la hipótesis alternativa
o la hipótesis alternativa  ,
y la decisión escogida coincidirá o no con la que en realidad es
cierta. Se pueden dar los cuatro casos que se exponen en el siguiente
cuadro:
,
y la decisión escogida coincidirá o no con la que en realidad es
cierta. Se pueden dar los cuatro casos que se exponen en el siguiente
cuadro: es cierta es cierta |
 es cierta es cierta |
|
|---|---|---|
Se escogió  |
No hay error (verdadero positivo) | Error de tipo II (β o falso negativo) |
Se escogió  |
Error de tipo I (α o falso positivo) | No hay error (verdadero negativo) |
Si la probabilidad de cometer un error de tipo I está unívocamente
determinada, su valor se suele denotar por la letra griega α, y en las
mismas condiciones, se denota por β la probabilidad de cometer el error
de tipo II, esto es:
En este caso, se denomina Potencia del contraste al valor 1-β, esto es, a la probabilidad de escoger  cuando esta es cierta
cuando esta es cierta
 cuando esta es cierta
cuando esta es cierta.
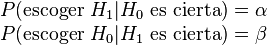
No hay comentarios:
Publicar un comentario