Distribución Binomial

En estadística, la distribución binomial es una distribución de probabilidad discreta que mide el número de éxitos en una secuencia de n ensayos de Bernoulli independientes entre sí, con una probabilidad fija p de ocurrencia del éxito entre los ensayos.

Un experimento de Bernoulli se caracteriza por ser dicotómico, esto es, sólo son posibles dos resultados. A uno de estos se denomina éxito y tiene una probabilidad de ocurrencia p y al otro, fracaso, con una probabilidad q = 1 - p. En la distribución binomial el anterior experimento se repite n veces, de forma independiente, y se trata de calcular la probabilidad de un determinado número de éxitos. Para n = 1, la binomial se convierte, de hecho, en una distribución de Bernoulli.

Para representar que una variable aleatoria X sigue una distribución binomial de parámetros n y p, se escribe:

• Su función de probabilidad es

donde

siendo las combinaciones de en ( elementos tomados de en )

Ejemplo

Supongamos que se lanza un dado 50 veces y queremos la probabilidad de que el número 3 salga 20 veces. En este caso tenemos una X ~ B(50, 1/6) y la probabilidad sería P(X=20):

Relaciones con otras variables aleatorias

Si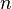 tiende a infinito y es tal que el producto entre ambos parámetros tiende a , entonces la distribución de la variable aleatoria binomial tiende a una distribución de Poisson de parámetro .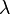
Por último, se cumple que cuando n es muy grande (usualmente se exige que ) la distribución binomial puede aproximarse mediante la distribución normal.

Propiedades reproductivas

Dadas n variables binomiales independientes,deello sale de parámetros n_i (i = 1,..., n) y , su suma es también una variable binomial, de parámetros n₁+... + n_n, y , es decir,