En estadística la distribución exponencial es una distribución de probabilidad continua con un parámetro  cuya función de densidad es:
cuya función de densidad es:
 cuya función de densidad es:
cuya función de densidad es:
Su función de distribución es:
Donde  representa el número e.
representa el número e.
 representa el número e.
representa el número e.
El valor esperado y la varianza de una variable aleatoria X con distribución exponencial son:
La distribución exponencial es un caso particular de distribución gamma con k
= 1. Además la suma de variables aleatorias que siguen una misma
distribución exponencial es una variable aleatoria expresable en
términos de la distribución gamma.
Se pueden calcular una variable aleatoria de distribución exponencial  por medio de una variable aleatoria de distribución uniforme
por medio de una variable aleatoria de distribución uniforme  :
:
 por medio de una variable aleatoria de distribución uniforme
por medio de una variable aleatoria de distribución uniforme  :
:
o, dado que  es también una variable aleatoria con distribución
es también una variable aleatoria con distribución  , puede utilizarse la versión más eficiente:
, puede utilizarse la versión más eficiente:
 es también una variable aleatoria con distribución
es también una variable aleatoria con distribución  , puede utilizarse la versión más eficiente:
, puede utilizarse la versión más eficiente:
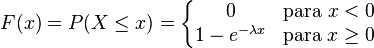
![E[X]=\frac{1}{\lambda}, \qquad V(X)=\frac{1}{\lambda^2}](http://upload.wikimedia.org/wikipedia/es/math/2/3/2/2320ae9816a49c79129829740a87c504.png)


No hay comentarios:
Publicar un comentario