Distribución Binomial Negativa


En estadística la distribución binomial es una distribución de probabilidad discreta que incluye a la distribución de Pascal.
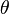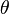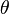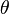El número de experimentos de Bernoulli de parámetro \theta independientes realizados hasta la consecución del k-ésimo éxito es una variable aleatoria que tiene una distribución binomial negativa con parámetros k y \theta.
La distribución geométrica es el caso concreto de la binomial negativa cuando k = 1.

Su función de probabilidad es
\! \ b^*(x;k,\theta) = {x-1 \choose k-1}\theta^k(1-\theta)^{x-k}
para enteros x mayores o iguales que k, donde
\!{x-1 \choose k-1} = \frac{(x-1)!}{(k-1)!(x-k)!}.
Su media es
\!\mu = \frac{{k(1 - \theta )}}{\theta}
si se piensa en el número de fracasos únicamente y
\!\mu = \frac{{k}}{\theta}
si se cuentan también los k-1 éxitos.
Su varianza es
\!\sigma ^2 = \frac{{k(1 - \theta )}}{{\theta ^2 }}
en ambos casos.
  • Si la probabilidad de que un niño expuesto a una enfermedad contagiosa la contraiga es 0,40, ¿Cuál es la probabilidad de que el décimo niño expuesto a la enfermedad sea el tercero en contraerla? En este caso, X es el número de niños expuestos la enfermedad y
\!x = 10, k = 3, \theta = 0,\!40
La solución es:
\!b^*(10;3,0,\!4)={10-1 \choose 3-1}0,\!4^3(1-0,\!4)^{10-3}={9 \choose 2}0,\!4^3(0,\,6)^{7}=0,\!0645
En un proceso de manufactura se sabe que un promedio de 1 en cada 10 productos es defectuoso, ¿cual es la probabilidad que el quinto (5) articulo examinado sea el primero (1) en estar defectuoso?. La solucion es: X= articulos defectuosos P= 1/10 = 0,1 q= 1- 0,1 = 0,9 x= 5 ensayos K= 1 b*(5;1,0.1)=(5-1\1-1)(0.1)^1*(0.9)^5-1= b*(5;1,0.1)= 6.6% de probabilidad que el quinto elemento extraido sea el primero en estar defectuoso.


Publicado por

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)