En estadística, se llama intervalo de confianza
a un par de números entre los cuales se estima que estará cierto valor
desconocido con una determinada probabilidad de acierto. Formalmente,
estos números determinan un intervalo, que se calcula a partir de datos de una muestra, y el valor desconocido es un parámetro poblacional. La probabilidad de éxito en la estimación se representa con 1 - α y se denomina nivel de confianza. En estas circunstancias, α es el llamado error aleatorio o nivel de significación, esto es, una medida de las posibilidades de fallar en la estimación mediante tal intervalo.
El nivel de confianza y la amplitud del intervalo varían
conjuntamente, de forma que un intervalo más amplio tendrá más
posibilidades de acierto (mayor nivel de confianza), mientras que para
un intervalo más pequeño, que ofrece una estimación más precisa,
aumentan sus posibilidades de error.
Para la construcción de un determinado intervalo de confianza es necesario conocer la distribución teórica que sigue el parámetro a estimar, θ. Es habitual que el parámetro presente una distribución normal. También pueden construirse intervalos de confianza con la desigualdad de Chebyshov.
En definitiva, un intervalo de confianza al 1 - α por ciento para la estimación de un parámetro poblacional θ que sigue una determinada distribución de probabilidad, es una expresión del tipo [θ1, θ2] tal que P[θ1 ≤ θ ≤ θ2] = 1 - α, donde P es la función de distribución de probabilidad de θ.
Intervalo de confianza para la media de una población
De una población de media  y desviación típica
y desviación típica  se pueden tomar muestras de
se pueden tomar muestras de 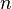 elementos. Cada una de estas muestras tiene a su vez una media (
elementos. Cada una de estas muestras tiene a su vez una media ( ). Se puede demostrar que la media de todas las medias muestrales coincide con la media poblacional:
). Se puede demostrar que la media de todas las medias muestrales coincide con la media poblacional: 
 y desviación típica
y desviación típica  se pueden tomar muestras de
se pueden tomar muestras de 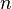 elementos. Cada una de estas muestras tiene a su vez una media (
elementos. Cada una de estas muestras tiene a su vez una media ( ). Se puede demostrar que la media de todas las medias muestrales coincide con la media poblacional:
). Se puede demostrar que la media de todas las medias muestrales coincide con la media poblacional: 
Pero además, si el tamaño de las muestras es lo suficientemente grande, la distribución de medias muestrales es, prácticamente, una distribución normal (o gaussiana) con media μ y una desviación típica dada por la siguiente expresión:  . Esto se representa como sigue:
. Esto se representa como sigue: 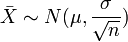 . Si estandarizamos, se sigue que:
. Si estandarizamos, se sigue que: 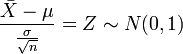
 . Esto se representa como sigue:
. Esto se representa como sigue: 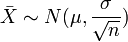 . Si estandarizamos, se sigue que:
. Si estandarizamos, se sigue que: 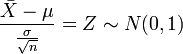
En una distribución Z ~ N(0, 1) puede calcularse
fácilmente un intervalo dentro del cual caigan un determinado porcentaje
de las observaciones, esto es, es sencillo hallar z1 y z2 tales que P[z1 ≤ z ≤ z2] = 1 - α, donde (1 - α)·100 es el porcentaje deseado (véase el uso de las tablas en una distribución normal).
Se desea obtener una expresión tal que ![P\left[\mu_1 \le \mu \le \mu_2\right] = 1 - \alpha](http://upload.wikimedia.org/wikipedia/es/math/2/5/9/2597bda8b576cec7c2e001ba5acf68ed.png)
![P\left[\mu_1 \le \mu \le \mu_2\right] = 1 - \alpha](http://upload.wikimedia.org/wikipedia/es/math/2/5/9/2597bda8b576cec7c2e001ba5acf68ed.png)
En esta distribución normal de medias se puede calcular el intervalo
de confianza donde se encontrará la media poblacional si sólo se conoce
una media muestral ( ),
con una confianza determinada. Habitualmente se manejan valores de
confianza del 95 y del 99 por ciento. A este valor se le llamará
),
con una confianza determinada. Habitualmente se manejan valores de
confianza del 95 y del 99 por ciento. A este valor se le llamará  (debido a que
(debido a que  es el error que se cometerá, un término opuesto).
es el error que se cometerá, un término opuesto).
 ),
con una confianza determinada. Habitualmente se manejan valores de
confianza del 95 y del 99 por ciento. A este valor se le llamará
),
con una confianza determinada. Habitualmente se manejan valores de
confianza del 95 y del 99 por ciento. A este valor se le llamará  (debido a que
(debido a que  es el error que se cometerá, un término opuesto).
es el error que se cometerá, un término opuesto).
Para ello se necesita calcular el punto  —o, mejor dicho, su versión estandarizada
—o, mejor dicho, su versión estandarizada  o valor crítico— junto con su "opuesto en la distribución"
o valor crítico— junto con su "opuesto en la distribución" 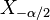 . Estos puntos delimitan la probabilidad para el intervalo, como se muestra en la siguiente imagen:
. Estos puntos delimitan la probabilidad para el intervalo, como se muestra en la siguiente imagen:
 —o, mejor dicho, su versión estandarizada
—o, mejor dicho, su versión estandarizada  o valor crítico— junto con su "opuesto en la distribución"
o valor crítico— junto con su "opuesto en la distribución" 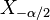 . Estos puntos delimitan la probabilidad para el intervalo, como se muestra en la siguiente imagen:
. Estos puntos delimitan la probabilidad para el intervalo, como se muestra en la siguiente imagen:
Dicho punto es el número tal que:
![\mathbb{P}[\bar{x} \ge X_{\alpha/2}] = \mathbb{P}[z \ge z_{\alpha/2}] = \alpha/2](http://upload.wikimedia.org/wikipedia/es/math/2/f/5/2f5137a79bb13690d3aaf86398000e39.png)
Y en la versión estandarizada se cumple que:

Así:
![\mathbb{P}\left[-z_{\alpha/2} \le \frac{\bar{x} - \mu}{\frac{\sigma}{\sqrt{n}}} \le z_{\alpha/2}\right] = 1 - \alpha](http://upload.wikimedia.org/wikipedia/es/math/2/5/d/25d23e4d3898de73cf6be54255482201.png)
Haciendo operaciones es posible despejar  para obtener el intervalo:
para obtener el intervalo:
 para obtener el intervalo:
para obtener el intervalo:![\mathbb{P}\left[\bar{x} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \le \mu \le \bar{x} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}}\right] = 1 - \alpha](http://upload.wikimedia.org/wikipedia/es/math/a/f/c/afced7770d053961a86781913ede1059.png)
De lo cual se obtendrá el intervalo de confianza:

Obsérvese que el intervalo de confianza viene dado por la media muestral  ± el producto del valor crítico
± el producto del valor crítico  por el error estándar
por el error estándar  .
.
 ± el producto del valor crítico
± el producto del valor crítico  por el error estándar
por el error estándar  .
.
Si no se conoce  y n es grande (habitualmente se toma n ≥ 30):
y n es grande (habitualmente se toma n ≥ 30):
 y n es grande (habitualmente se toma n ≥ 30):
y n es grande (habitualmente se toma n ≥ 30): , donde s es la desviación típica de una muestra.
, donde s es la desviación típica de una muestra.
Aproximaciones para el valor  para los niveles de confianza estándar son 1,96 para
para los niveles de confianza estándar son 1,96 para  y 2,576 para
y 2,576 para  .
.
 para los niveles de confianza estándar son 1,96 para
para los niveles de confianza estándar son 1,96 para  y 2,576 para
y 2,576 para  .
.Intervalo de confianza para una proporción
El intervalo de confianza para estimar una proporción p, conocida una proporción muestral pn de una muestra de tamaño n, a un nivel de confianza del (1-α)·100% es:

En la demostración de estas fórmulas están involucrados el Teorema Central del Límite y la aproximación de una binomial por una normal.

No hay comentarios:
Publicar un comentario