En estadística el tamaño de la muestra es el número de sujetos que componen la muestra extraída de una población, necesarios para que los datos obtenidos sean representativos de la población.
Objetivos de la determinación del tamaño adecuado de una muestra
- Estimar un parámetro determinado con el nivel de confianza deseado.
- Detectar una determinada diferencia, si realmente existe, entre los grupos de estudio con un mínimo de garantía.
- Reducir costes o aumentar la rapidez del estudio.
Por ejemplo, en un estudio de investigación epidemiológico la determinación de un tamaño adecuado de la muestra tendría como objetivo su factibilidad. Así:
- Si el número de sujetos es insuficiente habría que modificar los
criterios de selección, solicitar la colaboración de otros centros o
ampliar el periodo de reclutamiento. Los estudios con tamaños muestrales
insuficientes, no son capaces de detectar diferencias entre grupos,
llegando a la conclusión errónea de que no existe tal diferencia.
- Si el número de sujetos es excesivo, el estudio se encarece desde el
punto de vista económico y humano. Además es poco ético al someter a
más individuos a una intervención que puede ser menos eficaz o incluso
perjudicial.
El tamaño de una muestra es el número de individuos que contiene.
Una fórmula muy extendida que orienta sobre el cálculo del tamaño de la muestra para datos globales es la siguiente:
n = ( (k^2) * N*p*q) / ( (e^2 * (N-1) )+( (k^2) * p*q))
N: es el tamaño de la población o universo (número total de posibles encuestados).
k: es una constante que depende del nivel de confianza que asignemos.
El nivel de confianza indica la probabilidad de que los resultados de
nuestra investigación sean ciertos: un 95,5 % de confianza es lo mismo
que decir que nos podemos equivocar con una probabilidad del 4,5%.
Los valores k más utilizados y sus niveles de confianza son:
k 1,15 1,28 1,44 1,65 1,96 2 2,58
Nivel de confianza 75% 80% 85% 90% 95% 95,5% 99%
(Por tanto si pretendemos obtener un nivel de confianza del 95% necesitamos poner en la fórmula k=1,96)
e: es el error muestral deseado. El error muestral es la diferencia
que puede haber entre el resultado que obtenemos preguntando a una
muestra de la población y el que obtendríamos si preguntáramos al total
de ella. Ejemplos:
Ejemplo 1: si los resultados de una encuesta dicen que 100 personas comprarían un producto y tenemos
un error muestral del 5% comprarán entre 95 y 105 personas.
Ejemplo 2: si hacemos una encuesta de satisfacción a los empleados con un error muestral del 3% y el
60% de los encuestados se muestran satisfechos significa que entre el 57% y el 63% (60% +/- 3%) del
total de los empleados de la empresa lo estarán.
Ejemplo 3: si los resultados de una encuesta electoral indicaran que un partido iba a obtener el 55%
de los votos y el error estimado fuera del 3%, se estima que el porcentaje real de votos estará en
el intervalo 52-58% (55% +/- 3%).
p: proporción de individuos que poseen en la población la
característica de estudio. Este dato es generalmente desconocido y se
suele suponer que p=q=0.5 que es la opción más segura. q: proporción de
individuos que no poseen esa característica, es decir, es 1-p. n: tamaño
de la muestra (número de encuestas que vamos a hacer).
Altos niveles de confianza y bajo margen de error no significan que
la encuesta sea de mayor confianza o esté más libre de error
necesariamente; antes es preciso minimizar la principal fuente de error
que tiene lugar en la recogida de datos. Para calcular el tamaño de la
muestra suele utilizarse la siguiente fórmula:
Otra fórmula para calcular el tamaño de la muestra es:
n=(Nσ^2 Z^2)/((N-1) e^2+σ^2 Z^2 ) Donde: n = el tamaño de la muestra.
N = tamaño de la población.
σ= Desviación estándar de la población, que generalmente cuando no se
tiene su valor, suele utilizarse un valor constante de 0,5. Z = Valor
obtenido mediante niveles de confianza. Es un valor constante que, si no
se tiene su valor, se lo toma en relación al 95% de confianza equivale a
1,96 (como más usual) o en relación al 99% de confianza equivale 2,58,
valor que queda a criterio del encuestador. e = Límite aceptable de
error muestral que, generalmente cuando no se tiene su valor, suele
utilizarse un valor que varía entre el 1% (0,01) y 9% (0,09), valor que
queda a criterio del encuestador.
La fórmula anterior se obtiene de la fórmula para calcular la estimación del intervalo de confianza para la media:
X ̅-Z σ/√n √((N-n)/(N-1))≤μ≤X ̅+Z σ/√n √((N-n)/(N-1))
En donde el error es:
e=Z σ/√n √((N-n)/(N-1))
Elevando al cuadrado el error se tiene: 〖(e)〗^2=(Z σ/√n √((N-n)/(N-1)))^2 e^2=Z^2 σ^2/n (N-n)/(N-1)
Multiplicando fracciones: e^2=(〖Z^2 σ〗^2 (N-n))/n(N-1)
Eliminando denominadores: e^2 n(N-1)=〖Z^2 σ〗^2 (N-n)
Eliminando paréntesis: e^2 nN-e^2 n=〖Z^2 σ〗^2 N-〖Z^2 σ〗^2 n
Transponiendo n a la izquierda: e^2 nN-e^2 n+〖Z^2 σ〗^2 n=〖Z^2 σ〗^2 N
Factor común de n:
n(e^2 N-e^2+Z^2 σ^2 )=〖Z^2 σ〗^2 N
Despejando n:
n=(〖Z^2 σ〗^2 N)/(e^2 N-e^2+Z^2 σ^2 )
Ordenando se obtiene la fórmula para calcular el tamaño de la muestra:
n=(Nσ^2 Z^2)/((N-1) e^2+σ^2 Z^2 )
Ejemplo ilustrativo: Calcular el tamaño de la muestra de una población de 500 elementos con un nivel de confianza del 99%
Solución: Se tiene N=500, para el 99% de confianza Z = 2,58, y como no se tiene los demás valores se tomará σ=0,5, y e = 0,05.
Reemplazando valores en la fórmula se obtiene:
n=(Nσ^2 Z^2)/((N-1) e^2+σ^2 Z^2 )
n=(500∙〖0,5〗^2 〖∙2,58〗^2)/((500-1) 〖(±0,05)〗^2+〖0,5〗^2∙〖2,58〗^2 )=832,05/2,9116=285,77=286
 la varianza de la variable dependiente y la varianza residual por
la varianza de la variable dependiente y la varianza residual por  , el coeficiente de determinación viene dado por la siguiente ecuación:
, el coeficiente de determinación viene dado por la siguiente ecuación:


 un conjunto de n pares con abscisas distintas, y sea
un conjunto de n pares con abscisas distintas, y sea  un conjunto de m funciones linealmente independientes (en un espacio
vectorial de funciones), que se llamarán funciones base. Se desea
encontrar una función
un conjunto de m funciones linealmente independientes (en un espacio
vectorial de funciones), que se llamarán funciones base. Se desea
encontrar una función  de dicho espacio, o sea, combinación lineal de las funciones base, tomando por ello la forma:
de dicho espacio, o sea, combinación lineal de las funciones base, tomando por ello la forma: .
. . En concreto, se desea que tal función
. En concreto, se desea que tal función  empleando, como criterio de "mejor", el criterio del mínimo error cuadrático medio de la función
empleando, como criterio de "mejor", el criterio del mínimo error cuadrático medio de la función 

 que minimizan
que minimizan  también minimizan
también minimizan  , y podrán ser calculados derivando e igualando a cero este último:
, y podrán ser calculados derivando e igualando a cero este último: Siendo i=1,2, . . .,m
Siendo i=1,2, . . .,m , para i=1,2, . . .,m
, para i=1,2, . . .,m , para i=1,2, . . .,m
, para i=1,2, . . .,m ) siendo ésta verdadera en la población.
Es equivalente a encontrar un resultado falso positivo, porque el
investigador llega a la conclusión de que existe una diferencia entre
las hipótesis cuando en realidad no existe. Se relaciona con el nivel de
significancia estadística.
) siendo ésta verdadera en la población.
Es equivalente a encontrar un resultado falso positivo, porque el
investigador llega a la conclusión de que existe una diferencia entre
las hipótesis cuando en realidad no existe. Se relaciona con el nivel de
significancia estadística. aquí es el supuesto de que la situación experimental presentaría un
«estado normal». Si no se advierte este «estado normal», aunque en
realidad existe, se trata de un error estadístico tipo I. Algunos
ejemplos para el error tipo I serían:
aquí es el supuesto de que la situación experimental presentaría un
«estado normal». Si no se advierte este «estado normal», aunque en
realidad existe, se trata de un error estadístico tipo I. Algunos
ejemplos para el error tipo I serían: o la hipótesis alternativa
o la hipótesis alternativa  ,
y la decisión escogida coincidirá o no con la que en realidad es
cierta. Se pueden dar los cuatro casos que se exponen en el siguiente
cuadro:
,
y la decisión escogida coincidirá o no con la que en realidad es
cierta. Se pueden dar los cuatro casos que se exponen en el siguiente
cuadro: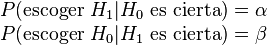
 .
. , donde
, donde 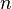 =número de sujetos en la muestra (también pueden ser representados por
=número de sujetos en la muestra (también pueden ser representados por  , donde
, donde  =número de grupos, cuando se realizan operaciones con grupos y no con sujetos individuales) y
=número de grupos, cuando se realizan operaciones con grupos y no con sujetos individuales) y  es el número de sujetos o grupos estadísticamente dependientes.
es el número de sujetos o grupos estadísticamente dependientes. son variables aleatorias, cada una de ellas con media
son variables aleatorias, cada una de ellas con media  , y que
, y que

 . La suma de los residuos (a diferencia de la suma de los errores, que no es conocida) es necesariamente 0,
. La suma de los residuos (a diferencia de la suma de los errores, que no es conocida) es necesariamente 0,
 (en este ejemplo, en el caso general a
(en este ejemplo, en el caso general a