La estadística inferencial es una parte de la estadística que comprende los métodos y procedimientos para deducir propiedades de una población estadística, a partir de una pequeña parte de la misma. La estadística inferencial comprende como aspectos importantes:
- La toma de muestras o muestreo.
- La estimación de parámetros o variables estadisticas.
- El contraste de hipótesis.
- El diseño experimental.
- La inferencia bayesiana.
- Los métodos no paramétricos
La Inferencia Estadística es la parte de la estadística
matemática que se encarga del estudio de los métodos para la
obtención del modelo de probabilidad (forma funcional y parámetros
que determinan la función de distribución) que sigue una variable
aleatoria de una determinada población, a través de una muestra
(parte de la población) obtenida de la misma.
Los dos problemas fundamentales que estudia la inferencia
estadística son el "Problema de la estimación"
y el "Problema del contraste de hipótesis"
Cuando se conoce la forma funcional de la función de distribución que sigue la
variable aleatoria objeto de estudio y sólo tenemos que estimar los parametros
que la determinan, estamos en un problema de inferencia estadística
paramétrica ; por el contrario cuando no se conoce la forma funcional
de la distribución que sigue la variable aleatoria objeto de estudio, estamos
ante un problema de inferencia estadística no paramétrica.
 la varianza de la variable dependiente y la varianza residual por
la varianza de la variable dependiente y la varianza residual por  , el coeficiente de determinación viene dado por la siguiente ecuación:
, el coeficiente de determinación viene dado por la siguiente ecuación:


 un conjunto de n pares con abscisas distintas, y sea
un conjunto de n pares con abscisas distintas, y sea  un conjunto de m funciones linealmente independientes (en un espacio
vectorial de funciones), que se llamarán funciones base. Se desea
encontrar una función
un conjunto de m funciones linealmente independientes (en un espacio
vectorial de funciones), que se llamarán funciones base. Se desea
encontrar una función  de dicho espacio, o sea, combinación lineal de las funciones base, tomando por ello la forma:
de dicho espacio, o sea, combinación lineal de las funciones base, tomando por ello la forma: .
. . En concreto, se desea que tal función
. En concreto, se desea que tal función  empleando, como criterio de "mejor", el criterio del mínimo error cuadrático medio de la función
empleando, como criterio de "mejor", el criterio del mínimo error cuadrático medio de la función 

 que minimizan
que minimizan  también minimizan
también minimizan  , y podrán ser calculados derivando e igualando a cero este último:
, y podrán ser calculados derivando e igualando a cero este último: Siendo i=1,2, . . .,m
Siendo i=1,2, . . .,m , para i=1,2, . . .,m
, para i=1,2, . . .,m , para i=1,2, . . .,m
, para i=1,2, . . .,m ) siendo ésta verdadera en la población.
Es equivalente a encontrar un resultado falso positivo, porque el
investigador llega a la conclusión de que existe una diferencia entre
las hipótesis cuando en realidad no existe. Se relaciona con el nivel de
significancia estadística.
) siendo ésta verdadera en la población.
Es equivalente a encontrar un resultado falso positivo, porque el
investigador llega a la conclusión de que existe una diferencia entre
las hipótesis cuando en realidad no existe. Se relaciona con el nivel de
significancia estadística. aquí es el supuesto de que la situación experimental presentaría un
«estado normal». Si no se advierte este «estado normal», aunque en
realidad existe, se trata de un error estadístico tipo I. Algunos
ejemplos para el error tipo I serían:
aquí es el supuesto de que la situación experimental presentaría un
«estado normal». Si no se advierte este «estado normal», aunque en
realidad existe, se trata de un error estadístico tipo I. Algunos
ejemplos para el error tipo I serían: o la hipótesis alternativa
o la hipótesis alternativa  ,
y la decisión escogida coincidirá o no con la que en realidad es
cierta. Se pueden dar los cuatro casos que se exponen en el siguiente
cuadro:
,
y la decisión escogida coincidirá o no con la que en realidad es
cierta. Se pueden dar los cuatro casos que se exponen en el siguiente
cuadro: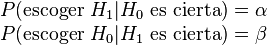
 .
.